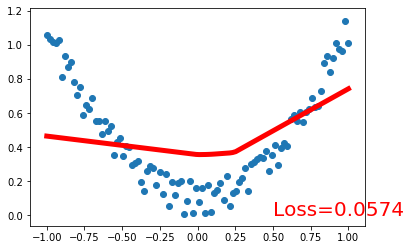
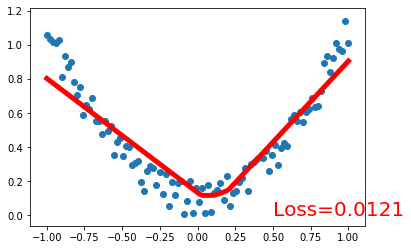
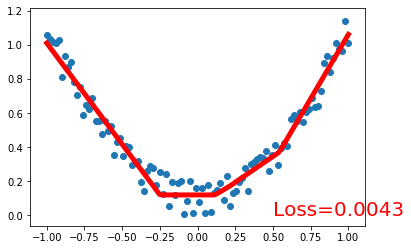
> 人工神经网络 VS 生物神经网络
Artificial Neural Nets Vs Neural Nets
相同与差别:
- 都有神经元
- 但是人工神经网络是固定不变的。
在训练过程中
- 生物神经网络会产生新的神经元,通过新的神经元来记忆信息
- 人工神经网络不会产生新的神经原,人工神经网络是预先准备大量正确数据,通过神经原的输出加工与正确数据进行对比,计算出loss值,在神经元中进行反向传递,从而修正神经元的强度,达到训练的目的。
- 即给定一个输入信号,和正确信息。输出信号通过神经元,到输出信号, 输出信号对比正确信息,计算loss梯度值, loss再进行反向传递,修改神经元强度,即修改神经元对正确信息有没有贡献
> 什么是神经网络(机器学习)
人工神经网络是一种数学模型
- 神经网络是一种运算模型,由大量的节点(或称神经元)之间相互联接构成
- 每个节点代表一种特定的输出函数,称为激励函数(activation function)
> 神经网络梯度下降
Gradient Descent In Neural Nets
- Optimization: Newton’s method, Least Squares method, Gradient Descent
- Cost = (predicted - real)^2 = (Wx - y)^2 = (Wx - 0)^2
> 激励函数
Activation Function
- Linear and NonLinear
- Y= Wx --> y = AF(Wx)
- AF : relu, sigmoid, tanh
- 当神经层只有两三层不是很多的时候任意的激励函数都行
- 卷积神经网络推荐的是relu
激励函数的使用
1 | import torch |
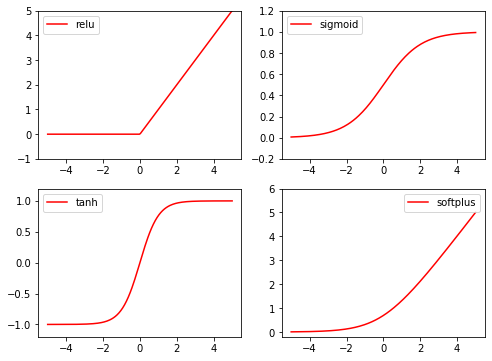
- 激励函数的使用:torch.tanh, torch.relu, torch.sigmoid, torch.nn.functional.softplus, torch.nn.functional.softmax
> Regression 回归
1 | # fake data 创建假数据 |